Best Guideline On How To Find A Cartesian Equation

If you are a college student pursuing mathematics, one of the common assignments will be dealing with Cartesian equations. The mere mention of the term “Cartesian equation” elicits anxiety among students, especially when they have a poor understanding of the fundamental theories. But you will no longer have to worry about Cartesian equations after reading this guide.
Table of Contents
What Is A Cartesian Equation?
The concept of the Cartesian equation was discovered by Rene Descartes, one of the greatest mathematicians of the 17th century. The discovery revolutionized the world of mathematics for offering the first link between Euclidean geometry and algebra.
The Cartesian coordinate system helps to establish any point in a plane using two main points, the x and y coordinates.
In order to define these points, you should draw two perpendicular lines and name them, as shown below:
Cartesian Equation Calculator
You might now be wondering how to find Cartesian equation. Before we get into any of the details of how it works, you might want to take a look at the Cartesian equation calculator before. There are many things to learn, such as concepts of converting a polar to Cartesian equation or how to find a Cartesian equation for the curve, but you might need a solution more quickly. So before you get into the concepts you can fill out your own problem to find a solution, to make things understandable for you. Do that with the helpful calculator below:
Converting Polar To Cartesian Equations
When students are faced with the assignments of solving polar equations, some of them look as if they are impossible to solve. To make your work easy, check the caption below that summarizes Cartesian and polar equations. Then, use the steps provided below the equation to do your calculations easily:
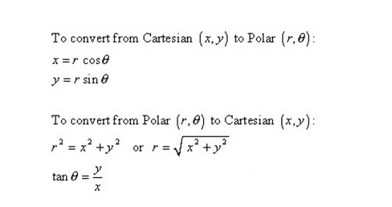
- Identify the current equation form
When you look at an equation, it should provide you with a clear indication it is in what form. If the equation contains something such as θs and rs, know it is a type of polar equation. But if it as ys and xs, it is in a rectangular or Cartesian form.Take the example; can you convert the following equation 5r=sin (θ). This must be a polar equation. Therefore, you should convert it to a Cartesian Equation - Clearly point out your main goal
If the problem you want to solve is in the form of a polar equation, the goal is converting to get the right ys and xs (Cartesian equation). But if it is in the form of a Cartesian equation, your focus is converting to rs and θs (polar equation). Understanding the goal is important to help you avoid getting stuck midway. - Carefully review the equation
Before you can start working on the conversion, take some moment to look at the main components. Then, follow the table below:For Polar equations, here is what to check For Cartesian equations, here is what to check R² X²+ y² Rcos(θ) X Rsin (θ) Y Taking a closer look at the equation 5r=sin (θ), you can convert it to what is on the right side by including an r term. Again, what is on the left-hand side can also be converted to what is in the right part by adding the r. So, we are going to multiply both sides by r to get the two equations below:
5r= sin (θ)
5r2= r sin (θ)
- Substitute your equation
Taking into consideration the second step, go ahead and start substituting.5r2= r sin (θ)
5 (x2+y2)= y
- Combine the like terms
The last step when converting polar equations to Cartesian equations is simplifying for similar figures. A fully simplified equation will easily express r in terms of θ or y in terms of x. In some cases, your teacher might require you to set RHS to zero for a truly simplified equation. The following three equations are in their varying degrees of simplification.5 (x2+y2) = y
5×2+ 5y2-y =0
5×2+y (5y-1)= 0
Your equation is now converted to a Cartesian equation. Another quick method is using the polar to Cartesian equation calculator. This one requires you to simply key in the polar components and get the results in the form of xs and ys. It is that simple. But the calculator can only be used to tell you the answer as opposed to demonstrating how you did it. So, it is important also to understand the entire process.
Converting Parametric Equations to Cartesian Equations
In some cases, your teacher might ask you to remove a specific parameter to solve for Cartesian equation of a curve. In this case, we are going to consider the equation x=e4t, y= t+9. So how do you find the Cartesian equation of a curve? Here are the main steps, done by a professional homework solver:
Process:
Start by eliminating the parameters in order to solve for Cartesian of the curve.
From our equation, x= e4t. Therefore, let us eliminate parameter t and then solve it from our y equation.
Y= t+9
y-9=t
x= e 4(y-9)
We can simplify this further.
Y=t+9
X= e4t
Let us move ahead and use the natural log of both sides of the equation. We will divide by 4.
lnx= 4t
lLnx/4= t
Now, we will plug our t parameter t back.
y=ln(x)/4 +9
If you check carefully, the equation is in the form of Cartesian coordinates.
Examples Of How to Find Cartesian Equation
The simplest method of finding Cartesian equation is using the Cartesian equation calculator. But you also need to understand how to find Cartesian equation. Here are some examples:
- Example 1: Find the Cartesian equation of the following equations
x = at2 (3)
y = 2at (4)To solve the equation, we know, (4), t = y/2a.
Therefore, we are going to substitute this into (3). So, it will look as demonstrated below.
x = a[y/2a]2
= y2/4a
Therefore y2 = 4ax - Example 2: Find the Cartesian equation from the following:
3r-cos2(θ)=sin2(θ)
From the equation, we can tell this is a polar equation. So let us rearrange the components.
3r-cos2(θ)=sin2(θ)
3r=sin2(θ)+cos2(θ)
Because we have two points, we can opt to multiply each side using r or square them. So, let us square each side to get the terms that can be converted easily.
(3r)2=12
9r2=1
Now, we can go ahead and substitute.
9r2=1
9(x2+y2)=1
The last step is combining the like terms before simplifying the equation. Here, note that the equation we get in the answer is for a circle that has a radius of 1/3. See the solution below.
9(x2+y2)=1
x2+y2=1/9
- Example 3: Find the Parabola equation from the following:
x2+3x+y2=6
First, it is important to appreciate that this is a rectangular equation. Therefore, the goal is to get a polar equation from the rectangular equation.
Taking a closer look at the equation above, we can categorize the parameters before converting them to r2.
x2+3x+y2=6
(x2+y2)+3x=6
Then, we finally substitute for all y and x terms, as demonstrated below.
(x2+y2)+3x=6
r2+3rcos(θ)=6
And we can simplify the process further. Note that this is not necessary unless you want to. Have a look.
r2+3rcos(θ)=6
r(r+3cos(θ))=6
And there we got it! Whenever you need to convert Cartesian to the polar equation, just follow those few steps.
Solving Cartesian Equations Simplified
This post has demonstrated that although many students consider finding Cartesian equations difficult, it does not have to be that challenging. All that you need to do when converting polar to the rectangular or Cartesian equation is following the steps we have provided. But if how to find Cartesian equation of a curve still appears difficult, and being able to convert polar to cartesian equation hard, it is time to look for help!
Using cheap math help provides you with a fast and reliable solution that guarantees you the best grades. Every paper you order is done by a professional who understands the math subject and has vast experience handling similar assignments. Whether you have a tight deadline or lack the right skills, there is no need to worry about your Cartesian equation homework. Just say “do my math homework for me” and let a professional help you!




















