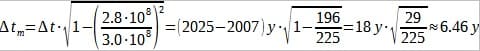Professional Homework Answers - Find Them Today!

3.2 Exercise Set (#1)

Solve. (2x − 3)(3x − 2) = 0

Answer: (2x - 3)(3x-2) = 6x² - 4x - 9x + 6 = 6x² - 13x + 6

3.3 Exercise Set (#41)

Height of a Ball. A ball is thrown directly upward from a height of 6 ft with an initial velocity of 20 ft / sec. The function s(t) = −16t2 + 20t + 6 gives the height of the ball, in feet, t seconds after it has been thrown. Determine the time at which the ball reaches its maximum height and find the maximum height.

Solution:

s(t) = −16t2 + 20t + 6

s(t) = -16(2)t + 20 = -32t + 20

maximum height occurs at s(t) = 0

-32t + 20 = 0

t = 20/32 = 0.625s

s(0.625) = -16(0.625)² + 20(0.625)+6 - 12.25 ft

Answer:

Time = 0.625 s

Max height = 12.25 ft

3.4 Exercise Set (#1)

Solve. 1/4 + 1/5 = 1/t

Solution:

1/4 + 1/5 = 1/t

1/4 + 1/5 = 9/20

1/t = 9/20

t = 20/9

4.1 Exercise Set (#49)

Dog Years. A dog’s life span is typically much shorter than that of a human. The cubic function d (x) = 0.010255 x3 − 0.340119 x2 + 7.397499 x + 6.618361,

where x is the dog’s age, in years, approximates the equivalent human age in years. Estimate the equivalent human age for dogs that are 3, 12, and 16 years old.

Solution:

d (x) = 0.010255 x3 − 0.340119 x2 + 7.397499 x + 6.618361

d (3) = 0.010255(3)^3 − 0.340119(12)^2 + 7.397499(12) + 6.618361 = 64.132

d (16)=0.010255(16)^3-0.340119(16)^2+7.397499(16)+6.618361 = 79.912

4.2 Exercise Set (#1)

State:

a) the maximum number of real zeros that the function can have;

b) the maximum number of x-intercepts that the graph of the function can have; and

c) the maximum number of turning points that the graph of the function can have.

f(x) = x5 − x2 + 6

Answer:

a) 1

b) 1

c) 2

Get Your Answer

Darth Vader would be 50 + 6.46 years old, i.e. 56 years, 5 months and 19 days.

Particle accelerator

Using the internet, find the location of a particle accelerator. In several paragraphs describe its size, what particles are being accelerated, how they are being accelerated, what their target is, how the particles are detected and what sub-atomic particles have been discovered at the site.

The Large Hadron Collider (LHC) at the Conseil Européen pour la Recherche Nucléaire (CERN) - also known as European Organization for Nuclear Research - in Geneva, Switzerland has a circumference of 27 km; assuming near circularity, its diameter is therefore ca. 8.6 km. It lies 50 - 175 m underground and is situated in a complex with multiple smaller accelerators; while the latter accelerate protons, antiprotons, negatively charged hydrogen ions and other ions, the LHC's purpose is the acceleration and collision of heavy ions and protons (CERN, 2009). The smaller accelerators intersection at specific points with the LHC and allow for the measurements of collisions of various elementary particles. For example, while the majority of the collisions are proton-proton collisions, heavier ions are also part of the experiments conducted at the LHC, which can include even lead-lead or lead-proton collisions. Hadron itself is a collective term for elementary particles, such as protons and neutrons, but also pions and kaons. These particles consist of quarks, which are held together by strong forces, lending integrity to the elementary particles.

A collider such as the LHC accelerates particles to near light speed and then lets them collide with one another; the collisions create new particles, which can then be studied. Thanks to the sometimes very short lifetime, these particles can only be studied when they are created de novo. In general, a proton collider such as the LHC has a reservoir of hydrogen gas; molecules and atoms from that gas are guided through an electromagnetic field, where they are separated from their electrons. The remaining protons are then accelerated using negative charges. To enable useful detection of newly generated particles during collisions, the protons are moved forward in discrete 'packages' and not via a continuous stream. The frequency of the electric field determines the width and speed of such packages. In addition, the accelerator has radiofrequency (RF) cavities in regular intervals, where radio waves interact with the proton bundles and further boost them forward. These waves also keep the protons on their way within the accelerator (CERN, 2019).

CERN follows different targets with the LHC; one of the main goals is the analysis of the question whether the mass of elementary particles is generated from symmetry breaking events that do or do not involve Higgs mechanisms; in addition, researchers would like to understand whether there are more dimensions accessible, and what the nature of dark matter may be.

Particles are detected in sensitive and complex detectors; electromagnetic fields inside those detectors trigger the particles to deviate from their trajectory. The curvature of the resulting - deviated - path can give important clues about the identity of the detected particle, as it depends on the particles momentum and charge. Moreover, calorimeters can measure the energy a particle loses while it deviates from its original flight path, and radiation detectors can detect any amount of radiation that the particle gives off while traveling with speeds faster than light through a specific medium.

The LHC has created several interesting findings and particles. For example, it has discovered quark-gluon plasma; it further detected a particle that is close to being the Higgs-Boson, although it needs to be independently confirmed.

Get Your Answer

The volume of the container can be calculated by

V = h*d*l

with h for height, d for depth and l for length.

The volume of the cylinder can be determined using the formula

V = h*π*((d²)/4)

with h for height and d for diameter.

After the lengths have been measured and the volumes calculated, the volumes will be measured by filling the containers with water and pouring the water into a measurement cylinder. We will then compare calculated and measured volume.

B. Volume

The volume of one drop will be measured by using an eye dropper and filling a graduated cylinder to the 1.00 mL mark and counting the drops; in a second round, the cylinder will be filled the same way from 1.00 mL to 2.00 mL. The number of drops will be averaged.

As an additional experiment, the volume of water in a plastic spoon will be determined by pouring water from such a spoon into the graduated cylinder; the average of two measurements will be determined.

C. Mass

Here, the average mass of five pennies will be determined to the milligram unit, using an electronic balance. In addition, the total mass of these five pennies on the balance will be determined by placing them all at once onto the balance.

3. Results and Discussion

A. Length and volume

The straight edged box has the following dimensions:

l = 12.5 cm; h = 14.0 cm; d = 19.5 cm.

Therefore, the volume of the box is

V(box) = 14.0 cm * 19.5 cm * 12.5 cm = 3,412.5 cm³

The drinking mug as cylinder yields the following measurements:

h = 9.5 cm; d = 7.7 cm.

Thus, the volume of the cylinder is

V(cylinder) = 9.5 cm * π * (7.7 cm ²)/4 = 442.4 cm³

Filling the containers with water and pouring it into a graduated cylinder yields the following volumina:

Vmeasured(box) = 3.391 L

Vmeasured(cylinder) = 0.420 L.

The measurements are smaller than the calculations, as not all water is completely transferred out of one into the other container, and it is difficult to fill the original box and mug completely, so they automatically have a smaller volume than calculated.

B. Volume

Using the eye dropper, it took 43 drops to fill the graduated cylinder to the 1.00 mL mark and 39 drops to fill it from 1.00 mL to 2.00 mL. Therefore, the average number of drops in one mL is

n = ½ * (43 + 39) = 41; the volume per drop is therefore

V(drop) = 1.00 mL / n * 0.02 mL.

This is in line with a general rule of thumb that assumes that a drop measures ca. 25 *L.

The volume in a plastic tea spoon was determined to be

V1 = 4.51 mL and V2 = 4.32 mL; the average value is therefore V average = ½ * (V1 + V2) or

V average = (4.51 mL + 4.32 mL) * 0.5 * 4.42 mL.

C. Mass

The five pennies were measured to be

2.176 g, 2.396 g, 2.424 g, 2.346 g, 2.188 g with an average of

m = 2.306 g.

If we place the pennies all at once onto the balance, we get

m = 11.550 g, which is almost the sum of all five pennies together; the actual sum would be 11.530 g, which means we have a deviation of 0.2%.

3. Conclusion

In all cases, the results met the expectation - by and large, with some unexpected findings. For example, when comparing measured to calculated volume, the measurements were distinctly smaller than calculated - this was surprising at first, yet made good sense, as we can't fill all devices completely. Measurement cylinders and other devices have actual graduations that do not aim at completely filling the device, so we always have to account for some 'dead' volume when filling a container. In that way, the experiments added a practical angle to our understanding of mass, length and volume. If one were to improve the experiments, one could combine mass and volume measurements by measuring the density of various liquids - alcohol, for example, will have a lower mass than water for the same volume.

4. Questions

1. The pencil is 8.70 cm long.

2A. Conversion factor: m/dm = 0.1 and dm/m = 10.
Therefore, 105 dm = x => x = 105 dm * m/dm = 105 * 0.1 m = 10.5 m
105 dm = 10.5 m.

2B. Conversion factors: g/mg = 0.001 and mg/g = 1,000.
Thus, 2,455 mg = x => x = 2,455 mg * g/mg = 2,455 * g * 0.001
2,455 mg = 0.002455 g.

Get Your Answer

The 95% confidence interval for heart rate mental arithmetic (M = 81.2924, SD = 13.61916) was calculated in SPSS. The 95% confidence interval was between 79.2836 and 83.3012. This information already offers a clue as to whether the heart rate during mental arithmetic is significantly different from the ‘standard’ heart rate of 72, as addressed in Question 2. Note that 72 is not within the confidence interval.

The readout was obtained through the Analyze Explore feature of SPSS, with heart rate mental arithmetic entered as the dependent variable.

Get Your Answer

import random, sys
# get field dimension validate the dimension before returning the value to main
def getField():
    while True:
        try:
            dim = int(input('Enter field size: (>=5): '))
            if dim>=5:
                field=[[0 for i in range(dim)]for j in range (dim)]
                return field
            else:
                print('Field size needs to be minimum of size 5')
        except:
            print('Invalid number. Please try again.')

# print the field
def printField(field):
    for row in field:
        for col in row:
            if col==0 or col==1:
                print('0',end=' ')
            elif col==-1:
                print('2',end=' ')
            else:
                print('8',end=' ')
        print()

# ask player to give up or enter row and column indices
def getplayerInput(field):
    dim=len(field)
    reply=int(input('Press 0 to give up or any number to continue. '))
    while reply!=0:
            row=int(input('Enter row {}-{} '.format(1,dim)))
            col=int(input('Enter column {}-{} '.format(1,dim)))
            if row<1 or row>dim or col<1 or col>dim:
                print('Invalid number')
                continue
            else:
                return row,col
    else:
        print('You have given up!')
        exit()

# takes in row and col index and field
# checks if the cell at row and col has 1
# if its 1 update it to -1
def hitAndValidate(field,row,col):
    hit=0
    miss=0
    if field[row-1][col-1]==1:
        print('Hit!')
        field[row-1][col-1]=-1
        hit=1
    elif field[row-1][col-1]==-1:
        print('Miss!')
        miss=1
    else:
        print('Miss!')
        field[row-1][col-1]='8'
        miss=1
    total=0
    # the sum of all the cells if is -5 then all targets has been hit
    for row in field:
        for col in row:
            if col is not '8':total+=col
    if total==-5:
        return True,hit,miss
    else:
        return False,hit,miss

# place random ship in the field
def placeShip(field):
    dim=len(field)
    toss=random.randint(0,1)
    if toss==0: # if its 0, the ship is placed horizontally
        row=random.randint(0,dim-1)
        col=random.randint(0,dim-5)
        for i in range(5):
            field[row][col+i]=1
    if toss==1: # else the ship is placed vertically
        row=random.randint(0,dim-5)
        col=random.randint(0,dim-1)
        for i in range(5):
            field[row+i][col]=1
# for player testing
def printField1(field):
    for row in field:
        for col in row:
            print(col,end=' ')
        print()

def main():
    print('Welcome to Battleship Game')
    field=getField() # get dimension from player and returns the field
    placeShip(field) # place a ship randomly either vertically or horizontally
    hits=0 # to store the number of hits
    misses=0 # to store the number of misses
    printField(field)
    while True:
        row,col=getplayerInput(field)
        result,hit,miss = hitAndValidate(field,row,col)
        hits+=hit
        misses+=miss
        printField(field)
        #printField1(field)
        if result:
            print('You have won!')
            break

main()

Get Your Answer

Solution:

The manager should choose the first investment project with a profit of $100,000 in each of the four years because the prevent value of the annuities for the first project is higher than that of the second project. In the case of the first project, the company will earn approximately $316,987 in present value over the next four years while the second project will yield a profit of approximately $237,740 in present value over the next six years.

Get Your Answer

Solution:

When evaluating a firm’s financial health and performance, it is important to use carefully selected financial ratios to determine how effectively it has been using its resources, how efficiently it has been managing its operations and how likely it is to meet its financial obligations. As the table below suggests, Starbucks’ profit margin and Return on Assets fell slightly between 2015 and 2017. Profit margin is a key profitability ratio that tells stakeholders how effective a firm is at converting sales into net income; an overly high profit margin ratio would indicate that operational expenses are too high (Thukaram, 2007, p.99). Return on Assets, on the other hand, helps determine how wisely and effectively a firm has been using its assets to generate revenue. In view of these considerations, it is evident that Starbucks’ operational effectiveness deteriorated slightly over the period being analysed, probably due to an increase in operational expenses – as the company opened hundreds of new stores between 2015 and 2017 (Starbucks, 2017).

As far as financial leverage is concerned, Starbucks’ debt-to-equity and debt ratios indicate that the company’s reliance on external debt increased rather significantly over the period being analysed. With that being said, its Return on Equity and Inventory Turnover ratios also rose rather considerably, meaning that both inventory and investors’ funds are being used in a very efficient manner (Gibson, 2012). Last but not least, Starbucks’ working capital ratio went from 1.08 in 2015 to 1.25 in 2017, which suggests that the company’s liquidity position improved significantly over the period being analysed.

A horizontal analysis of Starbucks’ 2015-2017 balance sheets reveals that the company experienced a significant increase in current assets (especially cash and cash equivalents and short-term investments) and a moderate increase in current liabilities, which explains why its working capital ratio rose by 0.17. As for its income statements, between 2015 and 2017 its total revenues rose by 17% whereas its net income grew by as little as 5%. This is because its operational expenses also went up, which means that management will have to do more to minimize waste and boost efficiency. A vertical analysis of the company’s 2015-2017 financial statements shows that while its liabilities-to-assets ratio grew from 53% in 2015 to 62% in 2017, most of its income statement items remained nearly unchanged – meaning that very little was done to cut costs and expenses.

Get Your Answer

The ruling aristocracy (also known as the patricians), allow the plebeians to appoint five key representatives (tribunes) in response to the protests. This decision sparks a sharp degree of anger within the proud soldier Caius Martius; a patrician who harbors nothing but hatred towards the lower class of people. While these events are taking place, a war starts with the neighboring tribe of Italians known as the Volscians. These Volscians are led by Tullus Aufidius; the rival of Caius Martius. Once the war concludes, the armies of Martius are declared the victor, Rome conquers the Italian state of Corioles, and the Volscians are ultimately defeated. To recognize the supreme leadership skills and war efforts of Caius, he is awarded the title of Coriolanus. Upon returning to Rome, the soldier is granted a hero's welcome; complete with an offer from the Senate to make him consul. This offer is granted only under the condition that he set out to win the votes of his estranged plebeians; a goal that he reluctantly accepts. Initially, the common folk agree to vote for him, yet their decision is later reversed when two tribunes known as Sicinius and Brutus manipulate the plebeians into believing that Coriolanus is an enemy of the people. Such treachery drives Coriolanus mad with rage, and he speaks out without filter against the concept of a popular vote. Using his shocking words as fuel for their argument, Coriolanus is declared a traitor to Rome and driven into exile.

Mutual Dislike Between The Plebeians And Coriolanus

Aside from the manipulation of the two tribunes, Coriolanus' indifference and disgust for the lower class were a major reason that they decided to rise against him; producing accusations of treason. As the plebeians were making their way to the Capitol, they were intercepted by Coriolanus' friend and fellow patrician Menenius; a man who attempted to speak to the mob and assure them that the patricians are working in their best interests. His method of persuasion was performed by comparing the role of the Roman Senate to the stomach's role in the human body. As the stomach exists as a storage container that houses and collects all the nutrients in the body, it then distributes them throughout. In a similar way, the patricians work to collect and subsequently distribute grain to the city's population. While the rioters and Menenius continue to argue, Coriolanus enters and proceeds to viciously curse the mob; labeling them nothing more than cowards and rabid dogs.

Manipulation of the Tribunes

During the events of Act III, Coriolanus is informed by Lartius that the Volscians led by Tullus Aufidius have raised an army against Rome; yet Coriolanus believes they are still too weak to mount any sort of meaningful attack. Upon learning of his rival's location in Antium, Coriolanus proceeds to see him there and begin the fight. Soon after, the scheming tribunes enter and are greeted with displeasure by Coriolanus. Subsequently, they announce that the plebeians have altered their votes in retaliation against Coriolanus, and state that he no longer has the permission necessary to become the consul. Knowing that their plans are simply an attempt to seize power, Coriolanus warns the Senators that they will never successfully rule over the people again if they allow for such an uproar to succeed. Sicinius and Brutus continue to attack the character of Coriolanus; increasing is anger at a rapid pace. Despite pleas to from both the senators and Menenius to calm him down, Coriolanus is unable to let go of his rage as foreseen by the tribunes; claiming that the people have been granted an excessive amount of freedom.

Additionally, he continues by saying that allowing them several privileges normally exclusive to nobles, they have become spoiled and greedy. He then insults the senators by claiming them fools to allow the deceptive tribunes to have a place on the political floor, stating that the people are unworthy of grain for remaining in the city during war time and bothering the state. Believing that the lower class folk must contribute in order to be awarded sustenance, he also condemns Brutus and Sicinius for their poor leadership and the plebeians for placing their trust in them. After their plans had finally come to fruition, the tribunes call for the common folk to confront and throw Coriolanus out of Rome. They answer the request while Menenius and the senators attempt to calm the stampeding crowd. One of the tribunes is granted the opportunity to speak and to assume more authority than ever before. Instead of helping to relax the people, Sicinius attempts to stir their fury even further; deeming that Coriolanus is a traitor to the people by committing treason via his hurtful remarks and therefore should be hurled off the Tarpeian rock. In his resistance attempt, Coriolanus claims that he would prefer to die an honorable death by fighting all of them.

Desiring to undergo a campaign of vengeance against Rome, the protagonist attempts to make peace with his rival in the city of Antium. Aufidius welcomes his assistance, and together their army proceeds to attack Rome; bringing the entire city under a state of panic as they are helpless against the overwhelming forces. Despite their strength, Coriolanus ultimately surrenders Antium's army at the request of his mother Volumnia, and is later assassinated by several henchmen belonging to Aufidius. No matter how strong of a leader, or how intelligent of a tactician, the pride of Coriolanus ultimately led to his downfall at every turn, and later, his tragic death.

Get Your Answer