Get better grades,
effortlessly.

Forget about deadlines, with top 2% experts across the board. Your high school and college homework assignments are not your problem anymore.

What Is A Transpose Matrix Calculator?

A matrix is a rectangular array of symbols, numbers, or expressions arranged in columns and columns. They are often used in computer graphics calculations, calculus, statistics, and numerical analysis among many others.

Matrix transposition denotes an operation that flips a matrix over its diagonal, and it is indicated with a "T" as an exponent. The result of this action is switching the row and column indices of a matrix.

For instance, when we transpose an m × n matrix, the result would be an n × m matrix.

Transpose of a Matrix Calculator – What You Need To Know

Before we get into using a transpose calculator, there are several aspects to consider:

The transpose of a square matrix, one with an equal number of rows and columns, is the most common
The transpose of 3x3 matrix is a matrix A^-1 such that A*A^-1and A^-1*A equal the identity matrix.
The transpose a 2x2 matrix can be considered as a mirrored version of it
Transpose of a matrix times the matrix gives the symmetric matrices.
The matrix inverse transpose is the transpose of the inverse matrix.

With these at your fingertips, using the online transposition calculator becomes as easy as ABC.

How To Find Transpose of a Matrix – Formula

In this part, we will look at three formulas that will help you find the transpose of the matrix painstakingly:

2x2 Transpose Matrix Formula

When we want to calculate the transpose of the matrix: 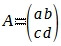the formula will be:

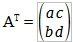
Transpose of 3x3 matrix

You can find the transpose of the matrix 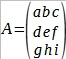by using the formula: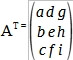

Transpose of 1 x 2 matrix

The transpose of matrix A = (a b) is from the formula below:

How To Find Transpose of a Matrix – Example

Calculate the transpose matrix of: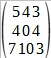

The solution to the problem will be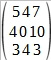

In short, finding the transpose means that the element at Row B Column Y of the original matrix is placed at Row Y Column B of the transpose matrix. The resulting element arc of the original matrix then becomes the element arc in the transposed matrix.

Multiplying a matrix by its transpose gives two square matrices. For instance, if A is an m × n matrix and AT is its transpose, then the solution would be AA^T is m × m and A^T A is n × n. The he product A^TA is a symmetric matrix.

How To Take The Transpose of a Matrix Using Our Calculator

Follow the steps below to achieve this:

Enter the elements of the matrices in the input fields (they must be real numbers)
Click on the "Submit" button to find the result
The answer appears in a new window

Do My Math Homework For Me

If you find the calculator inadequate, you can use our quality and cheap online help. Feel free to place your order now!